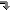Text Fragments

A text fragment is a fragment whose content is composed of text, and it is a primary component to compose your knowledge in a Piggydb database. The content can be formatted using a wiki-like markup syntax, as shown:
(Clicking the help button [?] shows the Wiki Markup Help.)
Piggydb puts the focus on the logical structure of knowledge rather than presenting information in a visually impressive way. So Piggydb provides just a minimal set of tools for simple formatting such as basic font decorations, lists, quotes, tables, etc. It does not provide a sectional level of text formatting because in Piggydb this is realized not in the content of a fragment, but with relationships among fragments and tags.

#pre tag / #code tag

Adding a #pre tag to a text fragment displays the content "as is" and no further formatting will be applied to it (similar to HTML <pre>..</pre> mark-up).
a sample fragment with #pre
Adding both #pre and #code tags to a text fragment displays the content "as is" with program-code syntax highlighting.
a sample fragment with #pre and #code
You can optionally specify the programming language in which the code is written with a #lang-<language name> tag, for more detail of language names, see the google-code-prettify document.

Preformatted text 

1
 2
  3
   4
    5

Program-code syntax highlighting 

/** 
 * The HelloWorldApp class implements an application that
 * simply prints "Hello World!" to standard output.
 */
class HelloWorldApp {
  public static void main(String[] args) {
    System.out.println("Hello World!"); // Display the string.
  }
}

Fragment Embedding

The text fragment formatting allows you to embed other fragments in the content of a text fragment.
A fragment embedded in another:

MathJax Support

LaTeX expressions in the content will be converted into mathematics notation by MathJax.

The Lorenz Equations

\[\begin{aligned} \dot{x} & = \sigma(y-x) \\ \dot{y} & = \rho x - y - xz \\ \dot{z} & = -\beta z + xy \end{aligned} \]

The Cauchy-Schwarz Inequality

\[ \left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) \]

A Cross Product Formula

\[\mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \end{vmatrix} \]

The probability of getting k heads when flipping n coins is

\[P(E) = {n \choose k} p^k (1-p)^{ n-k} \]

An Identity of Ramanujan

\[ \frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\ldots} } } } \]

A Rogers-Ramanujan Identity

\[ 1 + \frac{q^2}{(1-q)}+\frac{q^6}{(1-q)(1-q^2)}+\cdots = \prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+2})(1-q^{5j+3})}, \quad\quad \text{for $|q|<1$}. \]

Maxwell's Equations

\[ \begin{aligned} \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{aligned} \]